Vibration Isolation of Machinery Mounted On Rigid Foundations
Vibration isolation is a method of vibration control where the source of the vibration and the object or system to be protected are separated using mechanical or material means. In practice, this separation is achieved by the use of some isolation mechanism (active, semi active, or passive) to weaken the dynamic coupling between the source of vibration and the system.
This blog will cover:
1. Single-Degree-of-Freedom (SDOF) Vibration Isolation
The most common and economical approach to vibration isolation is by the use of passive systems (ex. rubber mounts), and it is isolation by passive means that will be the focus of our discussion.
Passive vibration isolation systems have the following advantages:
- Cost Efficiency
- Simplicity
- Availability
Cost Efficiency
Passive vibration isolations systems are almost always less expensive than active isolation systems that generally require servo-controls and auxiliary power source.
Simplicity
As alluded to with regard to cost efficiency, passive isolation systems are simpler, and thus more robust and reliable, in the sense that their behavior is more easily predictable and that they do not require the use of auxiliary power systems.
Availability
Unlike active and semi-active isolation systems, which often have to be built to purpose and subsequently can have longer lead times, Passive systems can often be “pulled off the shelf”. More often than not, an existing passive isolator can be readily applied to a range of different machines, reducing lead times, or eliminating them altogether.
For all of the advantages that passive vibration isolation systems have, they don’t work well for every type of system. Proponents of active vibration isolation systems are quick to point out examples such as the applications of active magnetic bearings in centrifuge rotors used in nuclear fuel processing, as well as specialized cryomachinery applications. A complete discussion of active magnetic bearings and active vibration control systems in general is well beyond the scope of this blog, but it suffices to say that there are highly specialized processes (ex. semiconductor manufacturing, uranium enrichment, cryogenic cooling) where the degree of vibration control required supersedes what passive systems are able to provide.
Single-Degree-of-Freedom (SDOF) Vibration Isolation
By separating or decoupling the source of vibration and the system upon which the vibration is induced, the passive isolation system (modeled as a spring and a damper in series attached to the system mass) the isolator (hopefully) achieves a reduction in vibration transmissibility. Assuming harmonic excitation, this reduction in transmissibility can be quantified with respect to either a reduction in transmitted force, or a reduction in transmitted motion. In both cases the transmissibility functions are mathematically identical:
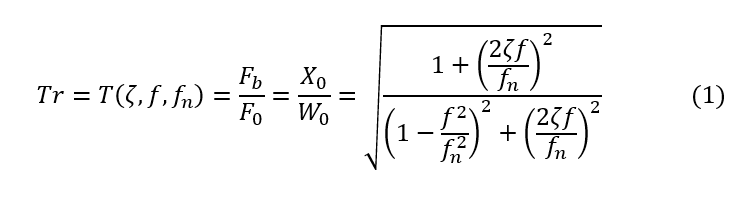
Where

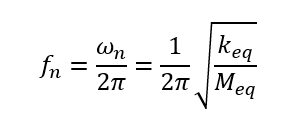
The parameters in the above equations are summarized in Table 1 below.
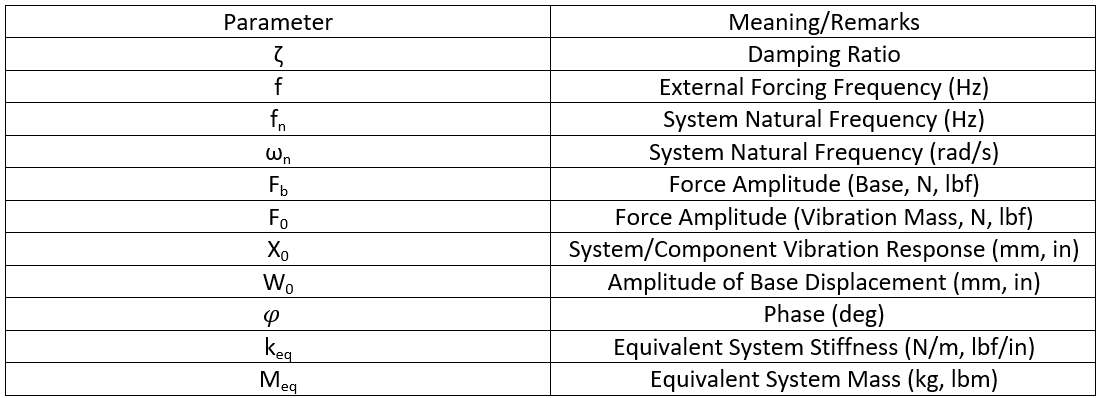
Table 1: Vibration transmissibility parameters
A simpler form, which reduces the functional dependence from three independent variables to two is shown below in Equation 2 and depicted graphically in Figure 1.
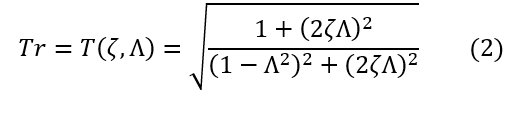
Where Λ is the frequency ratio f/fn. Figure 1 below is constructed using Equation 2.
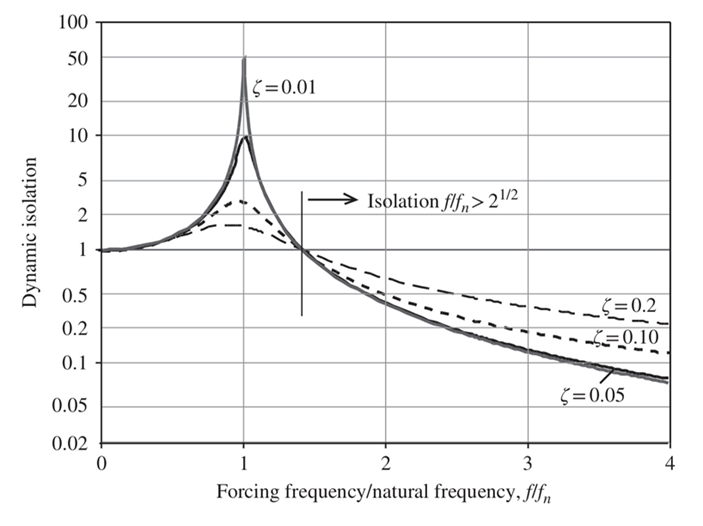
Figure 1: Dynamic isolation (transmissibility) as a function of natural frequency
Strictly speaking, the range (vertical axis) in Figure 1 isn’t telling the whole story. This is pointed out here because transmissibility and isolation, while closely related, are two distinct things, and need to be approached as such if an isolation problem is going to be quantified correctly. Transmissibility tells us how much of the excitation makes its way to the system. Isolation tells us how much of the excitation we’ve successfully prevented from getting to the system. Because the transmissibility is a dimensionless ratio, and (ultimately) because of the second law of thermodynamics, 100% of the excitation will not make its way to the system, that is, Tr < 1. Of course, if 96% of the excitation makes its way to the system we still have significant vibration problem, so the need to quantify isolation becomes readily apparent:
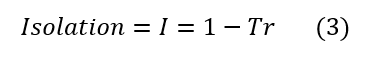
This humble equation is the key to many practical vibration isolation problems. We can think of it in any number of ways, but the bottom line is that it provides a way to directly quantify and optimize the level of isolation germane to the systems under consideration. This is best illustrated by an example.
Vibration Isolation of rooftop HVAC unit
We have the following data for a rooftop HVAC unit vibrating due to unbalance. The goal is to isolate the HVAC unit vibration and the resulting noise to the greatest extent practically achievable to prevent it being transmitted to a medical test facility situated immediately below.

Table 2: Rooftop HVAC unit data

Figure 2: Rooftop HVAC unit
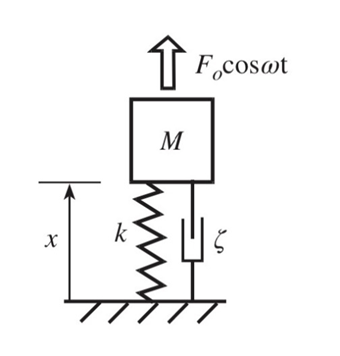
Figure 3: SDOF model of HVAC system (sinusoidal excitation)
We begin by determining the operating frequency in (Hz) from the operating speed:
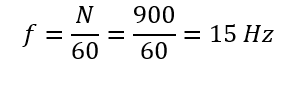
When the extent of transmissibility (not the damping) has a designated value on the order of 10-2, we can approximate the transmissibility function in Equations 1 and 2 by the following relation:
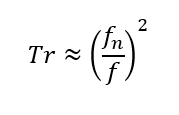
This approximation is additionally justified by virtue of the fact that in order to achieve “good” isolation at the operating frequency, the isolation/suspension system natural frequency fn has to be much lower than the input/excitation frequency, in this case the 15 Hz operating speed. This gives us the means to solve for the required isolator natural frequency directly:
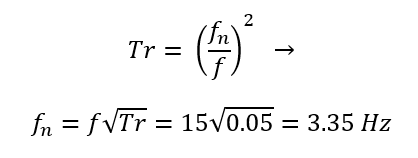
From here, we can estimate the required equivalent stiffness and static deflection of the isolator to achieve 5% transmissibility:
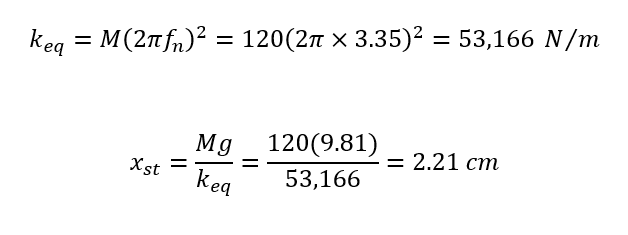
Lastly, we directly calculate the isolation from the given value of the transmissibility function:
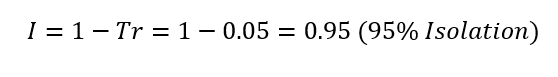
Having determined the required values, we can then go shopping for a set of isolators that would achieve the 95% isolation or proceed with the design of an isolation system that operates within the numerical bounds.
Conclusion
We’ve Shown how the direct application of simple SDOF vibration models can be used to quantify the extent of transmissibility and the effectiveness of the vibration isolator both in the abstract and in situations of applied interest. It is important to understand that the above methods are applicable only to those cases where a machine is mounted on a rigid foundation. In many cases of applied interest, the foundation is not rigid and is possessed of non-negligible mass/inertia as well as damping. This necessarily introduces at least one additional degree of freedom into the analysis. In future blogs the basic methods discussed here will be extended to cases of two or more degrees-of-freedom.
Feel free to check out my other related posts: