You have performed an essential (perhaps single-opportunity) test and taken the measurements you need to assess the specimen’s performance.
Is the data good… and useful?
How do we evaluate the validity of the data? We know that all experiments have measurement errors. Some data sets are worse than others. Some may simply be bad and should be discarded. Others may have errors/biases that can be “fixed."
In this post, I'll cover:
- Data Validity "Tests" and "Adjustments"
- The Test Environment: Pyroshock Testing
- The Use of Signal Velocity as a Data-Validity Test
- A Proposed Strategy to Reduce the Effects of the Errors
- Application of the Strategy to Several Data Sets
- References
- Software Download: Demonstration Software, Video Tutorial, and Pyroshock Data Set
Data Validity “Tests” and “Adjustments”
In many instances, an experienced investigator can assess data quality by “eyeball."
Goofy signals are often obvious from the time history. Others require a more discerning test.
If the data is “essentially correct in our view," can we make “adjustments” to improve its validity and usefulness. What does “adjustment” mean? Is it cheating? What is “legitimate”?
Some “corrections” are straightforward. Removal of the measured DC offset from an AC-coupled transducer is an easily recognized correction that is routinely performed. High- and low-pass filtering may be used to remove frequency components that we don’t care about. Other strategies may not be so straightforward.
This post discusses a test that is not only difficult to perform but one in which eyeball data validity checking is not adequate. A more discerning test is required.
The problem is discussed and an “adjustment” to “compromised but basically good” data is proposed.
The Test Environment: Pyroshock Testing

Figure 1: PyroShock Events
Responses from pyrotechnic events are notoriously hard to measure. These events are normally excited by explosives (Figure 1) but impacts can produce similar responses. The tests are very brief and may have high amplitude (thousands of Gs) and high frequency (up to 100 KHz) acceleration responses. They produce time histories like the one shown in Figure 2.
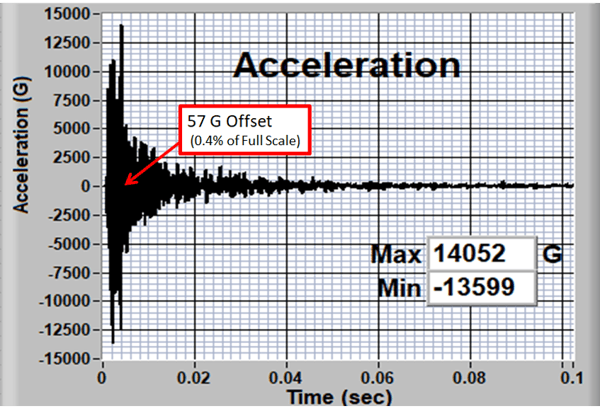
Figure 2: PyroShock Test Response
Examination of the signal by eye looks fine. In fact, it’s about as good as you can expect from a pyro test. But, it has a fatal error that makes normal analysis techniques (shock response spectrum (SRS) and energy-based analyses) fail. There is an offset of about 57G during the event. The offset is only 0.45% of the peak acceleration… a trivial error in most shock experiments.
The standard method of characterizing the damage potential of a shock waveform is the shock response spectrum (SRS).
When we perform an SRS analysis on the signal we get the result shown in Figure 3.
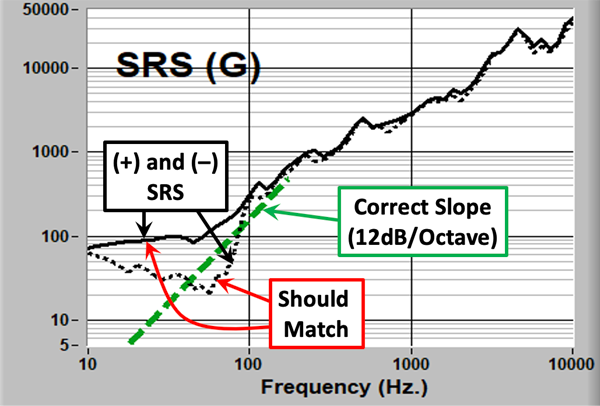
Figure 3: Shock Response Spectrum (SRS)
The SRS should have these characteristics:
- At low frequency (well below any structural mode activity) the slope of the SRS plotted in log-log form will be +2 (12dB/Octave). Deviation from this will indicate modal response at low frequency that does not exist.
- The positive and negative SRS results should be similar. (It is critical that both are calculated as a diagnostic).
The result shown obviously violates these criteria below 100 Hz. If we are interested in damage below that frequency this result is not acceptable.
The causes of these offsets have been discussed in Reference 1 and 2. The conclusion is that even when best practices are followed, the offsets occur because of non-idealities in the transducers and/or signal conditioning. The accelerometer and instrument vendors have done their best to reduce the effect, but it remains a significant problem.
The Use of Signal Velocity as a Data-Validity Test
Let’s look at the signal with a different analysis.
One of the things that we know is that, for most tests, the specimen is not moving very much at the end of the experiment. So, the velocity should be small at the end of the event.
We integrate the signal in Figure 2 from acceleration to velocity and get the result shown in Figure 4.
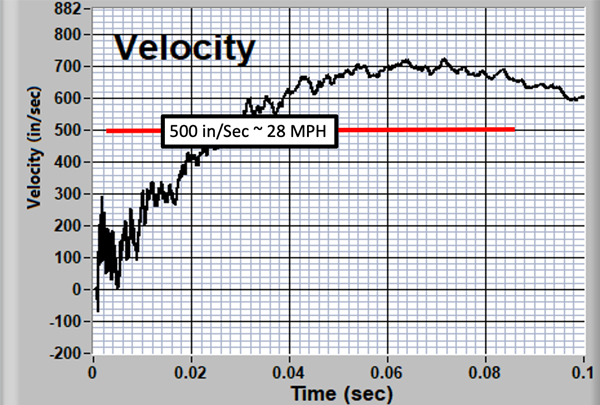
Figure 4: Signal Velocity
The velocity trace indicates that our specimen is headed through the laboratory wall. This is probably not true!
Velocity has been used for shock-data-quality assessment in many laboratories largely because of its promotion by Alan Piersol (Ref 3). The IES Recommended practices (Ref 4) states that the velocity offset should be less than the shock oscillation level (sometimes called the Piersol Criterion). The data in Figure 4 obviously violates this rule. In fact, much of the shock data acquired over the years is in violation until (often dubious) processing is done.
Note: The processes described here assume that the test article is at the same velocity (zero) at the beginning and end of the test. This is the case for many, but not all, shock tests. For example, for a drop test, where the specimen has an initial velocity but is stationary at the end, the processes described here would have to be modified to accommodate the different end conditions.
So, the velocity signal presents a very visible indication of the validity of shock data. The following discussion describes a technique that uses this velocity error to “correct” the problem.
It was developed for, and used in, the analysis of data acquired during a test series performed at National Test Systems (NTS), Santa Clarita in 2016 for PCB. A variety of commercially available shock accelerometers were subjected to high-level pyro events (Figure 5) and their responses were measured with a high-bandwidth, high-dynamic-range data acquisition system. The test series is described in Reference 5. The paper’s Appendix shows the results of all of the tests in plot form. Examination will show that almost all of the tests fail Piersol’s Criterion.

Figure 5: The PCB/NTS Test Specimen
A Proposed Strategy to Reduce the Effects of the Errors
For this discussion, we won’t worry about the source of the error. We will accept the fact that the offset errors occur, look at the result, and suggest and demonstrate a technique to mitigate the problem.
Several methods have been proposed to reduce the effect of these experimental errors: High-pass filtering (Ref 6) and wavelet correction (Ref 7). These approaches have shown some success but are far from universally applicable. This paper proposes a third method based on the brute-force characterization and subtraction of measurement errors.
The strategy proposed is a refinement of the technique described in Reference 8. It uses the fact that we have a very good estimate of the indicated velocity after the dynamics have settled down and that we know that it should be very close to zero at the end of the test. The strategy is to do our best to characterize the error and subtract it from the signal.
We make the following assumptions:
- The initial acceleration-measurement error is an offset that occurs near the time of peak response. If it is a true step, it would cause a straight-line velocity error starting at the step time. Examination of the test results shows that it is more complex than that. Further investigation might be appropriate.
- Deviations from the straight-line velocity after the shock are caused by drifts or the inherent AC-coupling of the transducer and signal conditioning.
The correction procedure is displayed in Figure 6:
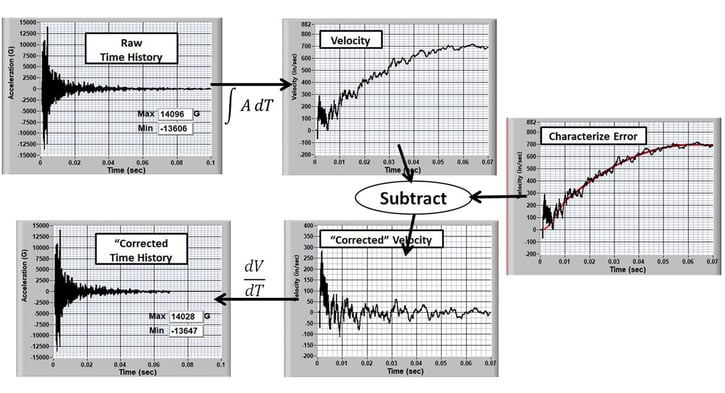
Figure 6: The Correction Process
- Integrate the acceleration data to obtain velocity.
- Characterize the velocity error.
- Subtract the velocity error from the raw velocity.
- Differentiate the corrected velocity to find the corrected acceleration.
Of course, the challenge is to characterize the velocity error accurately. For the strategy suggested here, an error-characterization curve, made up of three parts, is used:
- Zero, at the beginning of the transient.
- A low-order polynomial after the significant oscillation.
- A cubic spline to join the two.
Figure 7 shows the correction for the full analysis time period. Details of the correction curve are shown in the expanded view of the shock period in Figure 8.
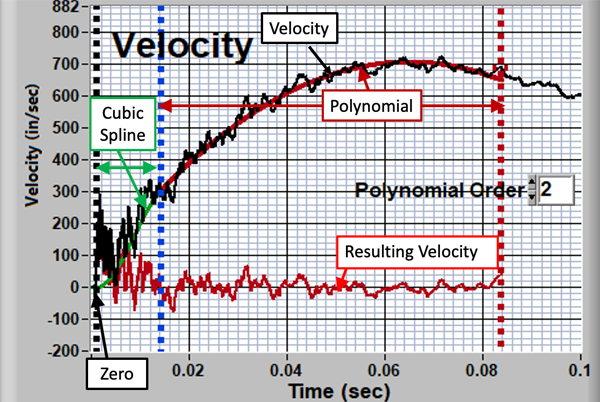
Figure 7: The Velocity-Fit Strategy
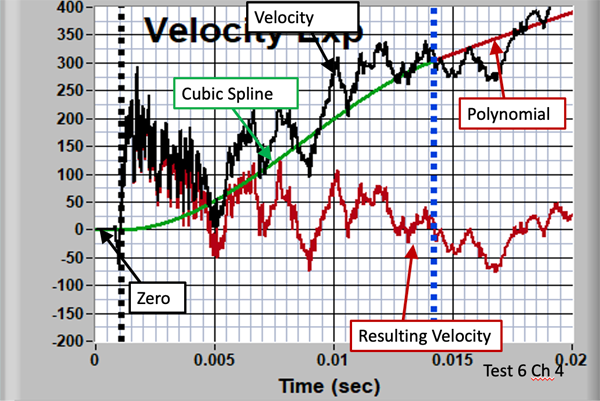
Figure 8: Expanded View in the Region of the Shock
The “tuning” parameters are:
- The degree of the polynomial. Second-order is almost always appropriate. Higher orders indicate that there are significant errors that are not associated with the assumed offset phenomenon.
- The period of the polynomial.
- The start time of the spline.
- The start time of the polynomial.
The primary objective is to optimize the velocity and SRS errors at low frequency. Care must be taken to not compromise the high-frequency result.
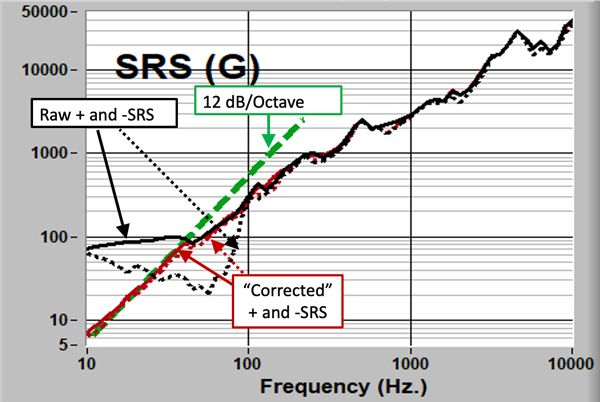
Figure 9: The Resulting SRS
This tuning results on the SRS shown in Figure 9. It can be seen that:
- The positive and negative SRS curves are essentially identical.
- The slope of the SRS at low frequency is very close to 12 dB/octave.
Obviously, the success of the correction depends on the tuning of the parameters. However, setting the cubic-spline range to cover most of the primary shock duration will usually work well.
The Appendix of Reference 3 shows results for all of the data acquired in the test series. (The tuning correction ranges were identical for all of the channels in a test, i.e. batch processing. Individual channel tuning might result in an improvement for some of the channels.)
Application of the Strategy to Several Data Sets
The results shown in the discussion above are from a PCB 350B01 (Test 4, Channel 4) mechanically isolated, electrically filtered (MIEF-IEPE) piezoelectric device that was analytically processed with a 2-pole, 2 Hz. high-pass filter.
Figure 10 shows the results from a PCB 350D02 (MIEF-EPE). The acceleration amplitudes are similar, but the velocity characteristic is significantly different: starting out positive and then going negative. Again, after appropriate adjustment, the correction is good.
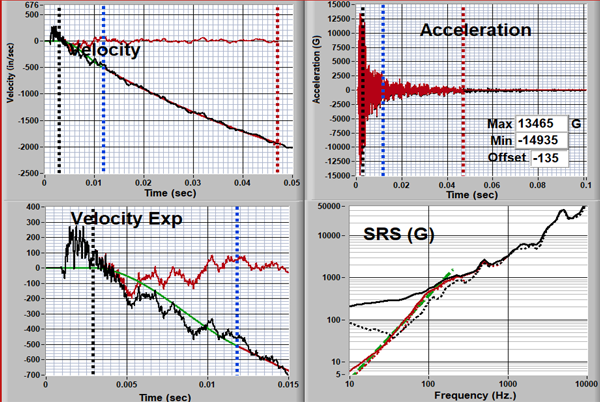
Figure 10: PCB 350D02 Result
On the other hand, the tool can make bad data look good. Figure 11 shows the results for a known bad channel (intermittent electrical connection). Despite the fact that the raw velocity shows suspicious behavior that is not obvious in the acceleration, appropriate (?) tuning makes it look good.
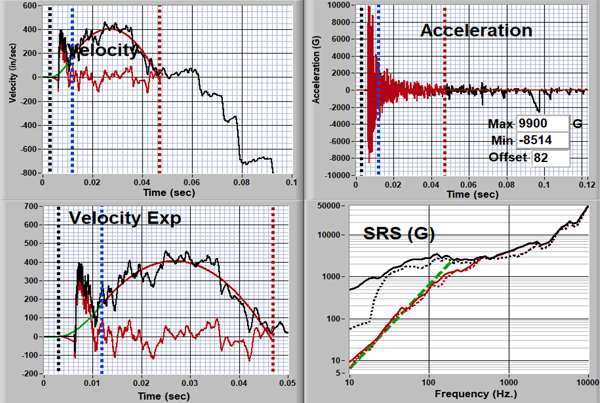
Figure 11: Bad Channel “Correction?”
References
Below is a list of the texts I reference throughout this post. A few (numbers 2, 3, 6, 7, and 8) are links to PDFs to you can download directly from this blog post.
- Anthony Agnello, Jeff Dosch, Robert Sill, Strether Smith, Patrick Walter: Causes of Zero Offset in Acceleration Data Acquired While Measuring Severe Shock,
- Strether Smith: The Effect of Out-Of-Band Energy on the Measurement and Analysis of Pyroshock Data, 2009 Sound and Vibration Symposium.
- Vesta Bateman, Harry Himelblau, Ronald Merritt: Validation of Pyroshock Data, Sound and Vibration Magazine March 2012
- IEST-RP-DTE032.2, Pyroshock Testing Techniques, Institute of Environmental Sciences and Technology, Arlington Heights, IL, 2009.
- Anthony Agnello, Robert Sill, Patrick Walter, Strether Smith: Evaluation of Accelerometers for Pyroshock Performance in a Harsh Field Environment,
- Bill Hollowell, Strether Smith and Jim Hansen: A Close Look at the Measurement of Shock Data--Lessons Learned— IES Journal 1992
- Smallwood, David O., and Jerome S. Cap: Salvaging Pyrotechnic Data with Minor Overloads and Offsets, Journal of the Institute of Environmental Sciences and Technology, Vol. 42, No. 3, pp. 27-35
- Strether Smith: Test Data Anomalies–When Tweaking’s OK, Sensors Magazine Dec 2003
Demonstration Software, Video Tutorial, and a Pyroshock Data Set
This process should offend any purists in the audience. However, if used judiciously, its success in making significantly flawed (but “good”) data usable should justify the means.
A software program that you can use to examine and manipulate a provided data set can be downloaded from Shock Correction (click to download Installer -- it will install immediately). It is an installable executable that will run on PCs.
For an overview of how to use this software, you can check out the following video and the Shock Correction Program Manual. You can also download an example data file.
- Shock Correction Program Manual (Click to Download)
- Example Pyroshock Data File CSV (Click to Download)
- Download this blog post as a PDF (Click to Download)
I hope you find this software useful, but please remember that it is, at this stage, simply a free tool for you to play with to correct shock-offset errors. Please contact me for feedback or any issues on the contact form that can be found here. Or, leave a comment below.
Related Blog Posts:
- All of Strether Smith's Blog Posts
- Shock Analysis: Response Spectrum (SRS), Pseudo Velocity & Severity
- 5 Minute Crash Course in Shock Analysis
Disclaimer:
Strether Smith has no official connection to Mide or enDAQ, a product line of Mide, and does not endorse Mide’s, or any other vendor’s, product unless it is expressly discussed in his blog posts.
