Vibration analysis is necessary to interpret your collected data in product tests, semiconductor manufacturing, certifying structural integrity, energy harvesting, and many other applications.
However, shock and vibration analysis is a difficult undertaking that presents engineers with a slew of formulas, methods, rules of thumb, and just plain confusion. How can you cut down on all the prep work and calculations involved and save time?
I've written this blog to answer these questions and to give you three foundational formulas that will help you save time while analyzing shock and vibration data.
For a deeper dive into analysis, I recommend checking out Tom Irvine's excellent 287-page PDF handbook An Introduction to Shock & Vibration Response Spectra. It can be downloaded for free in the Learn section on our enDAQ website. All of the chapters are available on our website as searchable pages as well.
Why is it so hard to get good data?
Each industry has obstacles that make obtaining good data challenging. Vibration analysis is as much an art as it is a science. Academic rules are your foundation when interpreting data, but you’ll occasionally need to rely on practical experience, too. You must understand the hazards of your test environment so that your components, systems, and structures can all be designed and tested accordingly.
For example, aerospace has countless examples of potential vibration problems:
- Helicopters may undergo "ground resonance" prior to takeoff
- Launch vehicles may have pogo oscillations in liquid engine propulsion systems
- Solid rocket boosters may have thrust oscillations
- Both high-performance aircraft and launch vehicles must withstand random
vibration due to turbulent boundary layers and shock waves as they accelerate
Ships, automobiles, machine tools, buildings, nuclear reactors, and other mechanical systems and structures all have their own vibration concerns and failure modes. These include yielding, buckling, ultimate stress, fatigue, fretting, fastener loosening, and more.
The Many Analysis Essentials
Vibration analysis involves many common aspects such as:
- Vibration excitation sources
- Shock types (including drop, seismic, pyrotechnic, water impact, etc.)
- Single-degree-of-freedom (SDOF) systems
- Damping
- Base excitation
- Sine sweep testing
- Fourier transforms (and Fast Fourier Transforms aka FFTs)
You’ll also need to determine the characteristics of the shock or vibration excitation so that you can properly analyze and test the affected components or structures. Only then can you make design modifications to avoid dynamic coupling between the excitation frequencies and the structure’s natural frequencies. These excitation sources can be grouped into four types:
- Initial Displacement or Velocity
- Applied Force
- Base Excitation
- Self-Excited Vibration
One way you can cut down analysis time is to use reference material listing formulas, methodologies, etc. with lots of examples. However, you’ll want to avoid becoming overwhelmed with textbooks, PDFs, and bookmarks, so rely on a few comprehensive sources when you’re still starting out. Again, I recommend Tom Irvine's handbook to give you a comprehensive overview of shock and vibration analysis.
Three Foundational Formulas
As an example of the sheer complexity involved in shock and vibration analysis, here are three widely-used formulas from Tom's handbook that will help you analyze your vibration data and obtain more meaningful results:
- Euler’s Equation: Euler’s equation is a complex exponential function used for Fourier transforms and for structural modal response. Complex exponentials such as these can simplify your trigonometry and save you time because they are easier to manipulate than their sinusoidal components.
Euler’s equation is:
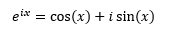
- Single-degree-of-freedom (SDOF) Response Equations: The equation of motion for base excitation is derived using Newton’s law. For support motion or seismic excitation, you can use the base excitation model and its free-body diagram:
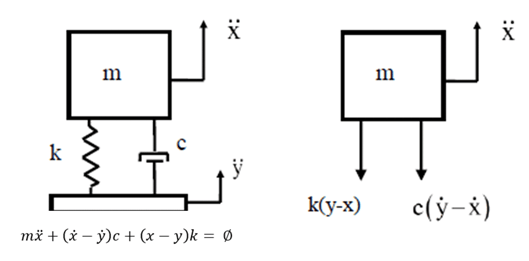
Here the base displacement is y, and base velocity is ẏ.
You can read more about Single-DOF Response Equations in the Single-Degree-of-Freedom Systems and Basic Concepts chapter of Tom's book.
- Fourier transform equations: The Fourier transform is a method for identifying the spectral content of a time history. Background equations include not only the pure mathematician approach but also the practical engineering version. As an example of the latter, the textbook Fourier transform X(f) for a continuous time series x(t) is defined as:
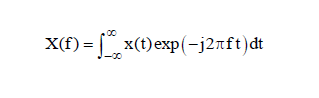
Note that j=√−1. Both the time and frequency domains are considered to extend from minus to plus infinity in their respective spheres.
Read Tom's chapter on Fourier Transforms for equations and examples.
Additional Formulas
Vibration analysis involves a staggering volume of mathematical tools and reference material. If you’re analyzing shock and vibration data in more than one application, it can be time-consuming to research the equations you’ll need. With this in mind, here are additional formulas you can use for your product tests, structural integrity analyses, and other applications:
- Bernoulli-Euler Beam Equations: If you’re working in a beam bending application, you can use the governing equation for beam bending free vibration which is a fourth order, partial differential equation.
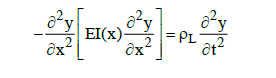
Here the term EI(x) is the stiffness which is the product of the elastic modulus and area moment of inertia, and ΡL is the linear mass density.
Read more about Bernoulli-Euler Beams here.
- Beam bending energy formulas: As a data analysis tool, you can derive natural frequency and modes shapes from a beam’s energy terms by using the Rayleigh-Ritz or finite element method. The following formulas are given for reference.
The total strain or potential energy P E of a uniform beam is:
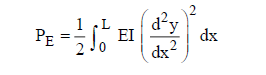
The total kinetic energy KE of a uniform beam is:
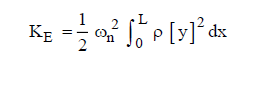
- Sine sweep time domain equations: If you’re working with linear sweep rates, you can use the normalized amplitude function for a linear sweep which is:
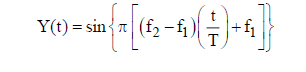Here the test duration is T. The starting and ending frequencies are f1and f2, respectively.
Check out Tom's extensive chapter on sine sweep testing.
- Miles equation for base excitation: The Miles equation is widely used due to its simplicity even though its assumption of white noise over an infinite domain does not actually exist in physical reality. A rule of thumb states that it may be used as long as the input PSD is flat within one-octave on either side of the natural frequency.
Consider an SDOF system subjected to base excitation where the input PSD is white noise over the frequency domain from 0 to infinity Hz. In cases like this you can determine the resulting RMS acceleration in g's by using the Miles equation:
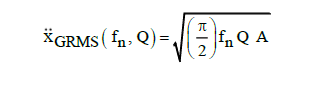
The constant power spectral density amplitude is represented by A with the unit of (G2/ Hz) and transmissibility at resonance is represented by Q.
A Single Source for Vibration Analysis
At enDAQ we want to help you save time spent on data analysis while ensuring you’ll get accurate data. Tom's handbook, An Introduction to Shock and Vibration Response Spectra, will help you bridge the gap between shock and vibration analysis as it’s taught in universities and as it’s practiced in industry. You’ll find formulas, advice and lots of examples to help you more quickly make sense of your data and verify your tests and designs.
Related Posts:
- Vibration Measurements: Vibration Analysis Basics
- Rating My Top 11 Vibration Data Loggers
- 6 Ways to Measure Vibration
For more on this topic, visit our dedicated Vibration Loggers & Vibration Sensors resource page. There you’ll find more blog posts, case studies, webinars, software, and products focused on your vibration testing and analysis needs.
